第１２回数理助教の会では数理第４研究室ポスドクの坂下達哉さんに「量子i.i.d.状態の仮説検定問題における数値的手法の実装および計算精度に関する研究」というタイトルでおはなししていただきました。
坂下さんは昨年９月に電通大で学位を取得され、現在、さきがけ数学領域「統計モデル多様体の普遍的な性質のベイズ予測理論への応用」の研究員としても精力的に研究を進めています。
坂下さんは、ここ数十年で急速な発展を遂げた量子情報科学の分野で、特に、量子仮説検定の問題に対して、数値的な取り扱いを研究しています。 実験的に準備された量子状態が、２つの異なる量子状態のどちらであるかを、統計的仮説検定の問題として判定する方法を考えています。通常の仮説検定論が情報理論の主要な結果に応用されているように、量子仮説検定論は量子情報理論への応用を念頭においたものになっています。 坂下さんが取り組んでいる量子Hoeffdingの定理の問題設定は数学的に精密な定式化で煩雑なため、ここでは、Hoeffdingの定理のイメージを簡単に説明しておきます。
たとえば、1/2の確率で表が出るコインAと2/3の確率で表が出る偽コインBがあり、コインをn回ふって判断することにします。 コインを１０回ふって６回表が出たときだと、AなのかBなのか判断に迷います。 しかし、コインをふる回数を１００回、１０００回と増やしていくと、表の出る確率は1/2 もしくは2/3に近づいていき判断しやすくなります。 いいかえるとコインがAの時とBの時とで、それぞれ間違った判断をする確率（誤り確率）が十分小さくなります。 コインをふる回数nに対して誤り確率は指数的に減少していくことが知られており、その速さを指数誤り率と呼びます。さて、コインAをコインBに間違えてしまう確率とコインBをコインAに間違えてしまう確率の間にはトレードオフの関係があります。2つの指数誤り率のトレードオフはHoeffdingの定理によって簡単な形で表現できます。このような仮説検定の漸近理論の量子版が、坂下さんが注目している量子Hoeffdingの定理で、２００６年に証明されたばかりです。
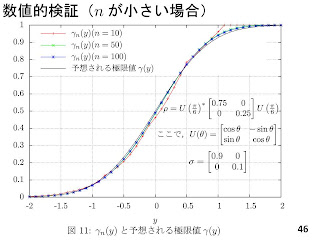
量子では試行回数ではなくテンソル積の次数nの極限を考え、指数誤り率は定理から簡明な形で書けますが、有限の場合には簡単にはかけません。 そこで、nが有限の場合の指数誤り率の振る舞いについて、数値的に詳しく調べたのが坂下さんの主要結果の一つです。
数値的に計算というと簡単そうに聞こえますが、この点について様々な工夫を行っています。本研究では、量子i.i.d.状態を表すテンソル積行列（指数サイズ）を多項式サイズの複数の行列に分解する「テンソル積の既約分解」という手法を用います。このような複数の行列に対して固有値計算が必要になるのですが、この計算で非常に大きな数値誤差が生じます。これは、このような行列では０の近くに固有値が密集しているためです。 この傾向は、nが大きくなるほど顕著になります。 実際、比較的小さなnでも、多倍長演算を用いて１００桁（10進法）程度で計算を行って、初めて有効な数値結果が得られています。計算機的にも非常にハードな計算ですので、 固有値ルーチンの改良、プロセス単位の並列化、そして、東大のスパコン（！）を用いてようやく可能になったそうです。数値計算の応用分野において、これほど大きな桁数を用いた固有値分解が必要な例は他になく、計算負荷を均等にする並列化法にも特色があり、数値解析や計算機実装の研究者にとっても面白いテーマを与えると思いました。
時間の関係で後半の一部は省略されましたが、最後に、新しい漸近理論に関する予想と数値的な検証について説明してもらいました。 既に示されている量子Hoeffdingの定理を用いて、数値計算が信頼できることを確認した後だからこそ検証に役に立つそうです。 数値的に試してうまくいくことを確認して、厳密な証明を与えるというのは、統計理論でもよくあるアプローチですが、 そこに量子論特有の難しさ（非可換な行列の扱いやテンソル積）が入っており、分野間融合の新しい可能性に溢れる話題だと思いました。
数理第４研究室 助教 ＆さきがけ数学領域研究者（兼任）田中冬彦
